5分で丸わかり！ 「債券」と「金利」の関係

なぜ「金利が上がれば債券価格は下がる」のか。簡単に言えば、金利が上がることで、すでに世の中に出回っている債券の魅力度が落ちるためだ。例えば、市場金利が2%の時、利率(クーポン)2%の債券Aがあったとする。金利が3%に上がり、クーポンが3%の債券Bが発行されたとする。残存年数(償還までの期間)が同じだとすると、あなたはどちらを選ぶか。当然、高いクーポンがもらえる債券Bを選ぶだろう。

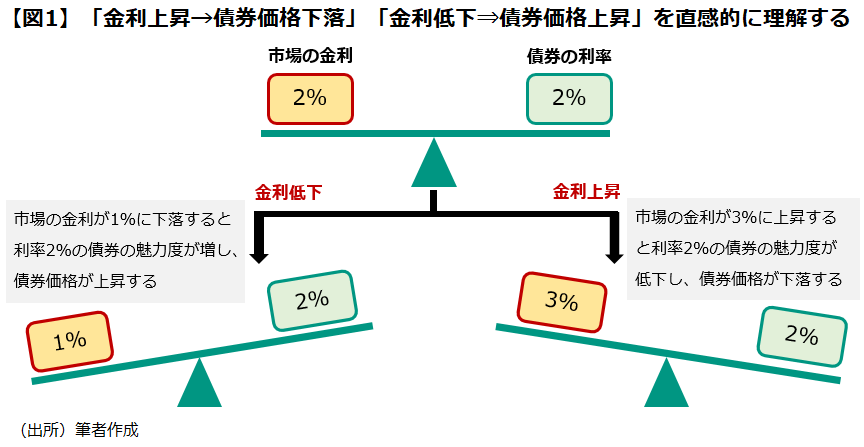
つまり、金融商品としての魅力度は「債券A＜債券B」となる。そのため、債券Aの価格は下がることになる。

それでは、金利上昇によって具体的にどのように債券価格が下がるのか。先ほどの債券Aと債券Bが、いずれも残存期間1年としよう。債券A保有者が1年間で得られるクーポンは2円。そして1年後に100円で償還される。債券価格が100円のままだとすれば、利回りは2%で、債券B(3%)に見劣りする。

債券Aにはクーポンの2円に加えて1円の「もうけ」が必要なわけだ。クーポンは固定なので、その1円は「値上がり益」として捻出するしかない。つまり債券Aが99円に値下がりすることで、償還時に1円(100円-99円)の値上がり益が発生する。そうして債券Aと債券Bはほぼ同じ魅力度になる。実際、購入価格(99円)に対するクーポン(2円)と値上がり益(1円)を合わせた額(3円)の利回りは約3%となる。

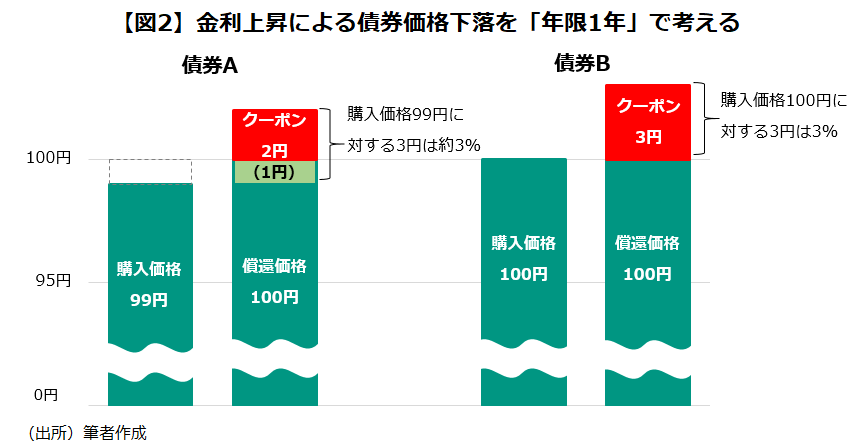
つまり「金利が1%上昇したことで、残存期間1年の債券の価格が約1%下落する」ことになる。

次にそれぞれの残存期間が5年だったとする。その場合、債券Aの値下がり幅はもっと大きくなる。なぜなら、残存期間が1年の場合と比べ、償還までの間に債券B保有者がもらえるクーポンが多くなるため、より多くの値上がり益が必要になるためだ。

債券Aは債券Bに比べ、クーポンが1円低いため、5年累積では5円、債券Bにクーポン収入で見劣りする。債券Aが債券Bと魅力度で肩を並べるためには値上がり益が5円あればよい。つまり、債券価格が95円になることで、償還額(100円)との差である5円の値上がり益が生まれ、魅力度で債券Bに近づくことになる。

ここまでの話は分かりやすさを優先したため、多少、大雑把な部分があることをご了承いただきたい(※1)。債券の利回りの尺度として最も使われる「最終利回り」でもしっかりと考えてみよう。最終利回りは満期まで持った場合のクーポンと値上がり益を含めた利回りのことで、以下の式で計算する(※2)。

仮に債券Aが95円に値下がりし、そこで購入したとしよう。上の式に当てはめると、

最終利回り＝{2+(100-95)/5}/95×100=3.16(%)

となり、債券Bの利回り(3%)に近づいているのが分かる。

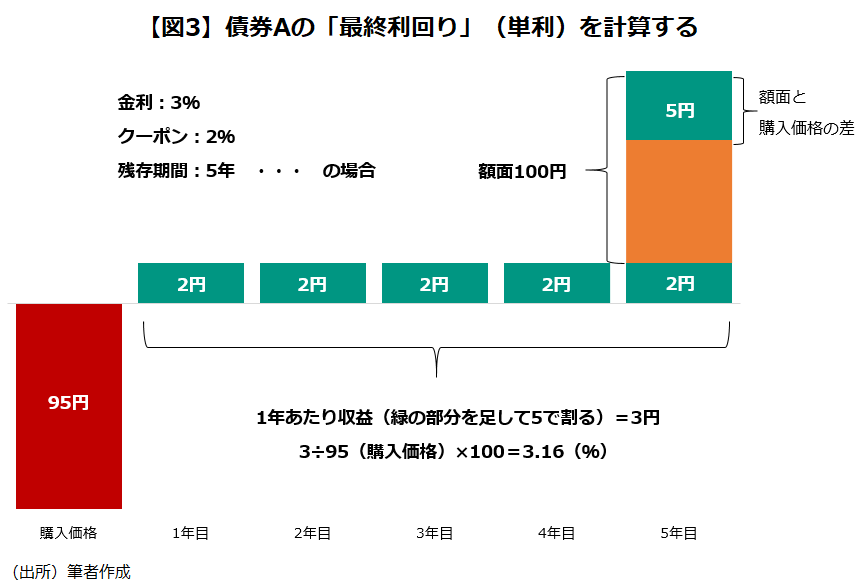
いずれにしても「金利が1%上昇したことで、残存期間5年の債券の価格が約5%下落する」ことになる。

残存期間が1年と5年の例を出したのは「残存期間が長くなるほど、金利が債券価格にもたらす影響が大きくなる」ことを説明したかったためだ。1%の金利上昇に対して、残存期間1年の場合は債券価格が約1%値下がり、残存期間5年の場合は債券価格が約5%値下がりしている。つまり、「金利上昇幅×残存年数」がおおよその「債券の下落幅」になっているのが分かるだろう。

より精緻な債券の時価は、クーポンおよび償還額というキャッシュフローの現在価値の合計から求める。多少、複雑になるので、この部分は読み飛ばしていただいて構わないが、様々な金融資産の価値評価に共通する重要なポイントではあるが、念のため、触れておきたい。

例えば、市場金利が3%だとする。現在の「100円」は1年後に「103円」になると考える。式にすると、100×(1+0.03)＝103円として導かれる。逆に、1年後の「103円」は現在の「100円」である。先ほどの式の逆算で考えればよい。103÷(1+0.03)=100円となる。この場合、「100円」を「現在価値」と呼び、「103円」を「将来価値」と呼ぶ。

2年後で考えると、100円の2年後の「将来価値」は100×(1+0.03)×(1+0.03)＝106円。2年後の106円の「現在価値」は106÷(1+0.03)÷(1+0.03)=100円である。この考えを応用し、将来のキャッシュフローを現在価値に割り引き、それらを合計することで「債券の現在価値」を求めることができる。

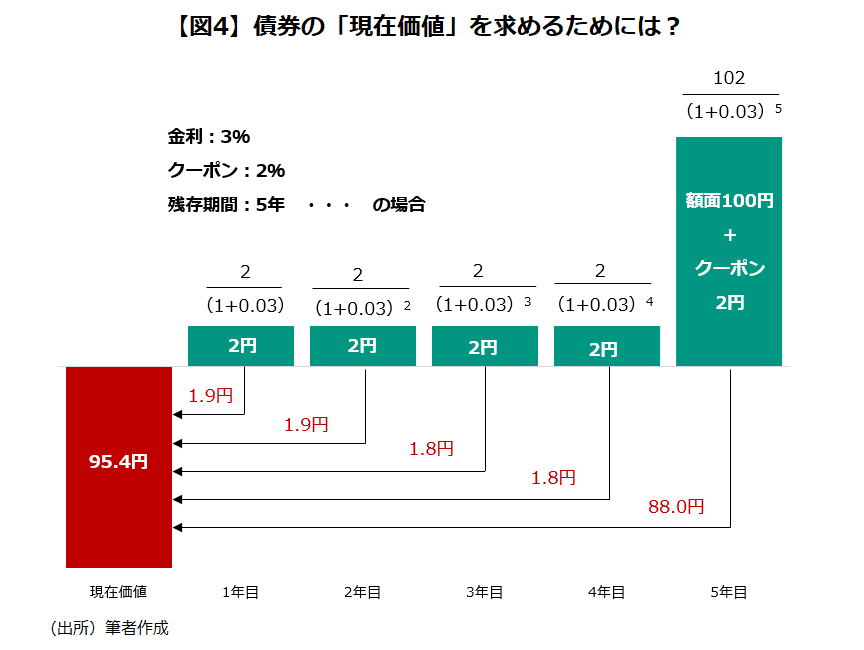
クーポン2%の債券Aの現在価値は、金利が1%上がった場合、上の図のように95円程度まで下がることがわかる。

先ほど「金利上昇幅×残存年数」がおおよその「債券の下落幅」になっていると説明したとおり、債券の残存年数は、金利変化がどのくらい債券価格に影響するか「感応度」を示している面がある。ただ実際の「金利感応度」は「デュレーション」という指標を使う。

デュレーションを一言で言えば「クーポンと償還額の平均回収年数」だ。クーポンは償還より前に債券保有者の手に渡るため、デュレーションは残存年数よりも通常、短くなる(デュレーション≦残存年数)(※3)。ただ、「平均回収年数」と聞いて、直感的に理解できる人は少ないだろう。残存年数とデュレーションの差は通常、そこまでかけ離れたものではないので、「残存年数のようなもの」がデュレーションだと覚えておけば問題ない。　

そもそも、債券は満期まで持ち切れば、(倒産などの信用リスクを考慮しなければ)額面で償還されるため、名目上の損失は生じない。ただ、個人がいつでも購入や売却が可能な債券ファンドは時価で評価するため、金利の動きはファンドの値段である基準価額にすぐに影響を与える。どのくらいの金利リスクを抱えているかという点で、「金利感応度」の概念を知っておく意義は大きい。デュレーションは月報などで確認できるため、債券ファンドを持っている人は定期的に確認してみるとよいだろう。

なお、個人向け国債を途中で換金する場合は、ここでの話とは異なり、経過利子などを踏まえて、受取額が決まる。財務省のウェブサイトで中途換金のシミュレーションができるので、必要に応じて確認してほしい。

最後に、金利と株価の関係にも触れたい。「金利が上がると株価が下がる」というワードを目にすることが多いが、果たして本当だろうか。

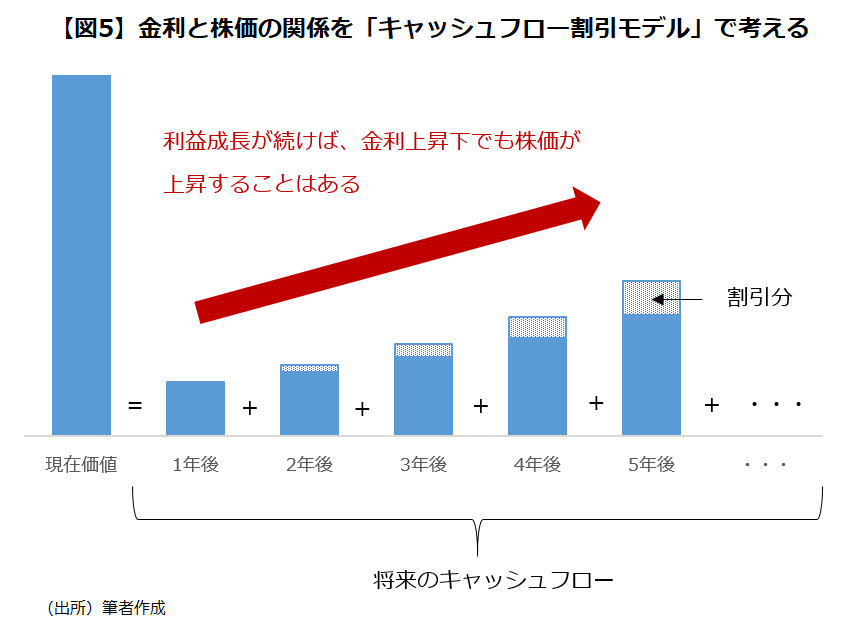
金利上昇そのものが株価にネガティブに働くというのは、大枠では誤りでない。株価は、その企業が将来生み出すキャッシュフローの現在価値(現在の事業価値)から求めることができる。この点は、前述の「債券の現在価値」と同じ考えだ。金利が上昇すれば、将来のキャッシュフローを現在価値に割り引く「割引率」が大きくなり、現在価値が小さくなる。すなわち、現在の企業価値が下がり、株価は下がる(※4)。

もっとも、債券のクーポンとは異なり、株式の生み出す将来のキャッシュフローは一定ではない。好景気や良いインフレを背景とした金利上昇の場合、企業の売上や利益の増加が見込まれ、金利上昇の悪影響を補って株価が上昇することもある。また、金融のように、金利上昇自体が業績にプラスの影響を与えるセクターもある。要するに、「金利と株価の関係」は、「金利と債券価格の関係」よりも複雑であり、一概には言えないところがある。

ちなみに、株式に対しても「デュレーション」という言葉を使うことがある。例えば、より遠い未来の利益成長を見込むグロース(成長)企業は投資額を回収するまでの期間、つまりデュレーションが長くなる。結果、グロース企業の株価の金利感応度は大きくなる。グロース企業が金利上昇に弱いとされる理由の1つである。