「ほったらかしは正解?」「積み立ては安全?」――直感のワナに注意!
「3囚人問題」はパラドックスか?
あなたは「3囚人問題」を知っているだろうか。「A」「B」「C」の3人の囚人がいる。彼らは重罪を犯しており、処刑を待つ死刑囚だ。ある時、恩赦によって、この中から1人が釈放されることが決まった。誰が釈放されるかはくじ引きで決まっており、明日、告げられる。結果が待てない「A」は看守にこのように聞いてみた。
「私は助かりますか」。
看守は「規則で、本人に伝えることは言えないし、誰が助かるかも言えない」という。あきらめきれない「A」は看守に、改めてこのように尋ねてみた。
「では、『B』か『C』のどちらかが処刑されるかは教えてくれませんか。これなら規則違反にはならないでしょう」。
看守は確かにその通りだと思い、「A」に「『B』は処刑される」と本当のことを伝えた。これを聞いた「A」は喜んだ。看守の発言を聞く前、自分が助かる確率は「1/3」だった。しかし、看守の発言によって「B」の処刑が固まった。つまり、助かるのは「A」(自分)か「C」の2人のうちの1人であり、確率は「1/2」に上がった、と考えたためだ。
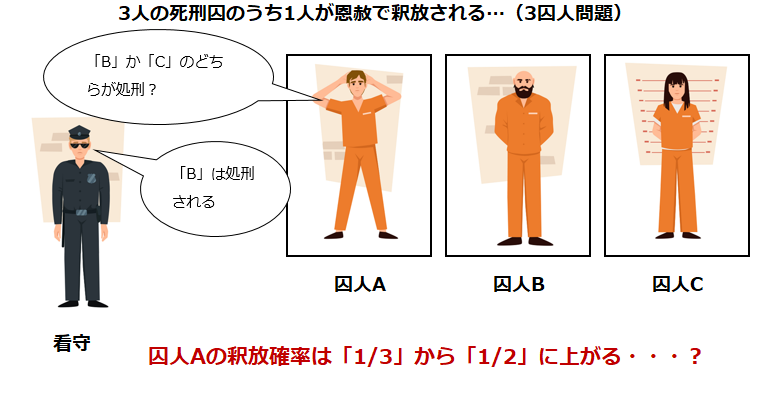
直感的に「A」の思考は正しいように思えるが、本当にそうだろうか。実は看守の話を聞いても、「A」が助かる確率は「1/3」のままなのである。
長期投資であればリスクを取って良いのか
なぜ「A」が助かる確率は「1/3」のままなのか釈然としない人は多いだろう。答えはコラムの最後にとっておく。まずは、人間の直感がいかにあてにならないかを分かってもらいたかった。そして、それを知っておくことは投資の世界でも非常に有益だ。さて、次のケースを考えてみよう。あなたは30代前半と若く、老後までに30年の時間があり、時間を味方につけた資産形成をしたいと考えている。専門家から以下のような投資のアドバイスを受けた時、どう感じるだろうか。
「運用期間が30年もあるのだから、リスクをとって株式100%のファンドに金融資産の大半を入れてほったらかし続けるのがいいよ」
「なるほど、確かにそうだ」と、直感的にアドバイスを正しいと受け取ってしまいがちだが、本当にそうか。少し疑った方がよい。理由は至ってシンプル。30年の運用期間があるとしても、本当に30年なのはスタート時点だけであり、15年過ぎれば運用期間は15年、29年過ぎれば運用期間は1年という短期になってしまうためだ。つまり、すべての投資期間において高いリスクを取り続けるのは正しいとは言えないのだ。
では運用期間が30年あったとして、どのように運用するのが正しいのかといえば、「その時々において適切なリスクを取ってリターンを追求すること」になる。もしも年齢によってリスク許容度が変わらないのであれば、資産分散などによって適切なリスクをとった一定の運用方法を続けるべきであるし、資産運用の外での「稼ぐ力」(いわゆる「人的資本」)が年齢や環境によって変わるならば、その都度、最適な資産配分を模索するのが正解になる。
もちろん、リスク許容度が高い投資家であれば、金融資産の大半を株式などリスクの高い資産で全期間、運用し続けてもよいだろう。ただし、「運用期間が長期だから」というのは大きなリスクを取る理由には実はならない。そして、運用期間が長期であることを理由にした「ほったらかし」は非常に危険な行為とも言えるのだ。
「積み立て投資」をコインのゲームにたとえると?
次に積み立て投資について考えたい。積み立て投資は資産形成手段としては非常に有効だと筆者は思っているが、誤解してはいけない部分がある。あなたは「積み立て投資はリスクを軽減する」という言葉を聞いたことがないか。直感的にそのまま受け入れてしまいそうだが、厳密に言えば、このフレーズは誤りである。
積み立て投資は本質的なリスク分散にならない。こちらも理由はシンプルで、「ひとつのゲームに賭けているから」だ。そのゲームは実際には全世界株やS&P500のインデックスファンドなりといった具合なのだが、単純化して以下のようなゲームとしてみよう。
【ゲームのルール】
コインの表が出たら掛け金が1.5倍、裏が出たら掛け金が半分になる
【ゲームの進め方】
最初の掛け金は1万円。2回目以降は前回の結果に1万円を加えて、賭ける
最初に運よく表が出て1万5000円になったとする。次の掛け金は、その1万5000円に1万円を足した2万5000円。今度は裏が出てしまい、1万2500円になってしまった。3回目はその1万2500円に1万円を足した2万2500円が掛け金となる。そこでコインの表が出たら3万3750円になる。さらに1万円を足して4万3750円を・・・という具合にゲームを続けていく。
ある時、掛け金が100万円になったとしよう(このようなキリの良い数字になるかは分からないが、その点はあまり本質ではないので無視する)。次、コインの裏が出たら、当たり前だが、半分の50万円になってしまう。
少々、単純化しすぎたきらいはあるし、実際の投資対象はここまでリスクが大きくないケースがほとんどだ。ただ定時定額の積立投資がやっていることは、このたとえと本質的に大きな差はない。私たちが生きている世界の物理法則において、同じ投資対象に投資しているのに、違うタイミングで投資した資金が同じ期間にそれぞれ違う動きをすることはない。ゲーム(=投資対象)が1つであるならば、本質的なリスク分散にならないというのはそういうことだ。
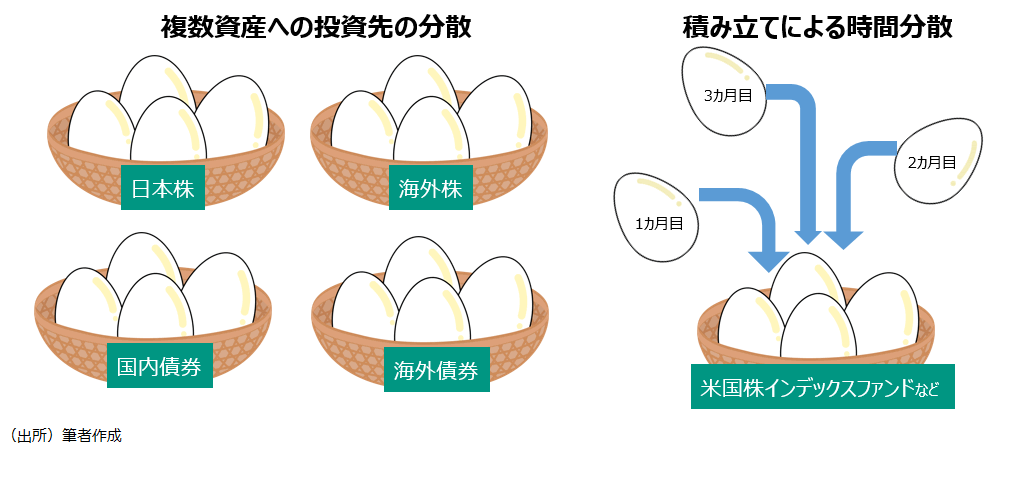
有名な投資の格言に「卵をひとつのカゴに盛ってはいけない」というものがあるが、積立投資がやっているのは、「ひとつのカゴに時間差で卵を盛る」ことなのだ。資産運用における本質的なリスク分散といえば、投資対象・資産の分散のことである。積み立てによる「投資タイミングの分散」はどちらかと言えば「心理的な負担を和らげる」という主観的な安心感を得る効果の方が大きい。
このように「直感」を疑うだけで、投資においても、新しいものの見方ができる。筆者も「分かりやすいこと」であるほど疑うようにしている。「分かりやすさ」は直感に訴えかけるが、直感は案外、あてにならないものであるためだ。
【3囚人問題】「A」の釈放確率はなぜ「1/3」のままなのか?
さて、冒頭の「3囚人問題」の話に戻りたい。なぜ、「B」が処刑されるという話を看守から聞いても、「A」が釈放される可能性は「1/3」のままなのか。「B」が釈放される可能性が0であるならば、「当初の『B』が釈放される可能性=1/3」はどこに消えたのか。実は「C」が釈放される可能性が「2/3」にあがったのだ。じっくりと考えてみよう。
最初の囚人らの釈放確率は以下の通りだ。
A ⇒ 1/3(約33%)
B ⇒ 1/3(約33%)
C ⇒ 1/3(約33%)
次に、看守が「B」が処刑されることを教えてくれた行動の意味するところを考えてみよう。
「A」が釈放される場合、看守は処刑される囚人について「B」と言っても「C」と言っても良い。「B」と言う確率は1/2(50%)だ。
「B」が釈放される場合、看守が、処刑されるのは「B」だという可能性は当然だが0%である。
「C」が釈放される場合、看守の選択肢は「B」が処刑されると伝えるしかない。つまり看守は100%「B」が処刑されると話すことになる。
当初、釈放される可能性が全員「1/3」だったのに、「『B』が処刑される」という情報が加わったことが意味するところは何か。「C」が助かる可能性が強いことを示唆していることに他ならないのだ。結果的に、釈放確率は以下のようになる。
A ⇒ 1/3(約33%)
B ⇒ 0/3(0%)
C ⇒ 2/3(約67%)
こうした確率は「ある情報が追加された場合、確率計算をし直す」というベイズ統計学で用いられる「条件付き確率」の計算で導き出すことができる(※補足も参照)。「3囚人問題」に似た命題に「モンティ・ホール問題」があるが、理屈は同じだ。
いずれにしても、「3囚人問題」は人間の直感や思い込みがいかにあてにならないかを教えてくれる好例といえる。
【補足】
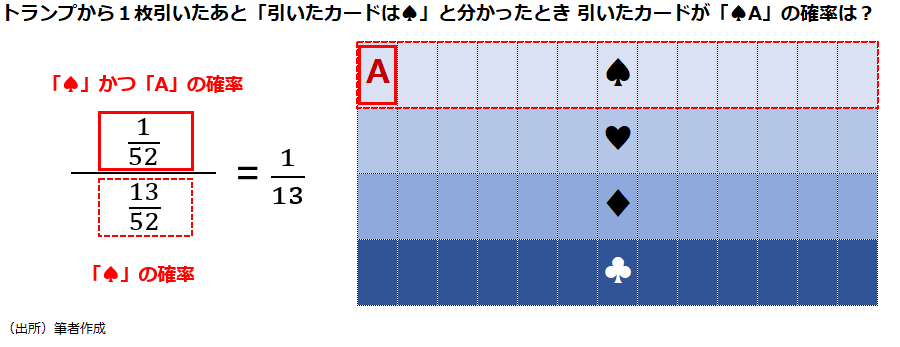
「条件付き確率」について補足した方がよいだろう。たとえば、あなたが52枚のトランプのカードの中から1枚のカードを引いたとしよう。当たりが「スペードのA(エース)」だとすると、それを引いた可能性は「1/52」だ。そこで「引いたカードはスペードだった」という情報が加わった。引いたカードが「スペードのA」である確率が「1/13」にアップするのはすぐに理解できるだろう。
この場合の「条件付き確率」の計算は「スペードのAを引く確率/スペードを引く確率」によって導かれる。具体的に式にすると以下のようになる。
(1/52)/(13/52)=1/13
トランプの例は単純であるが、「3囚人問題」もこの応用だ。「A」が釈放される確率は「『A』が釈放され、看守が『B』が処刑されると伝える確率(分子)/看守が『B』が処刑されると伝える確率(分母)」である。分子は「『A』が釈放される確率」とその上で「看守が『B』が処刑されると伝える確率」の掛け算であり、「1/3×1/2=1/6」である(先ほどのトランプの例における「スペードのA」の確率に相当)。
分母については、各囚人が釈放されるケースに分けて考えよう。看守が「B」が処刑されると伝える確率は、「A」が釈放される場合は「1/2」であり、「B」が釈放され場合は「0」であり、「C」が釈放される場合は「1」である。つまり「(1/3×1/2)+(1/3×0)+(1/3×1)」であり、計算すると「1/2」になる(先ほどのトランプの例における「スペード」の確率に相当)。「A」が釈放される確率は以下のように導き出される。
(1/6)/(1/2)=1/3
よって、「A」が釈放される確率は、看守の話を聞く前後で変わらないのである。

海老澤 界(えびさわ かい)
松井証券ファンドアナリスト
投資信託を多面的にウォッチし、豊富な投信アワードの企画・選定経験から客観的にトレンドを解説
<略歴>
横浜国立大学経済学部卒業後、日刊工業新聞記者を経て格付投資情報センター(R&I)入社。年金・投信関連ニューズレター記者、日本経済新聞記者(出向)、ファンドアナリストを経て、マネー誌「ダイヤモンドZAi」アナリストを務める。長年、投資信託について運用、販売、マーケティングなど多面的にウォッチ。投信アワードの企画・選定にもかかわる。日本証券アナリスト協会認定アナリスト。


