いつでも長期投資の味方か？ 一歩先行く「複利効果」論

「複利は人類最大の発明だ」――。天才物理学者、アインシュタインが残したとされる言葉として有名だ。以前、当コラムでも書いたが、筆者はこの出典を知りたいと考え、色々な文献をあたったが、見つけることはできなかった。真相はさておき、アインシュタインの名前が駆り出されるくらい、複利効果は投資(特に長期投資)において、重要視される概念といえよう。

複利効果を簡単に言えば、「リターンがリターンを生む」ということだ。「72の法則」を知っている読者の方も多いのではないか。複利効果を前提にした場合、資産を2倍にするために必要な「年数」と「利率」をかけるとおおよそ「72」になるというものだ。例えば、3%の利率で2倍にするためには「72÷3」で24年が必要だ。また、10年で2倍にしたいのだったら「72÷10」で7.2%の利率で運用しなければならない。

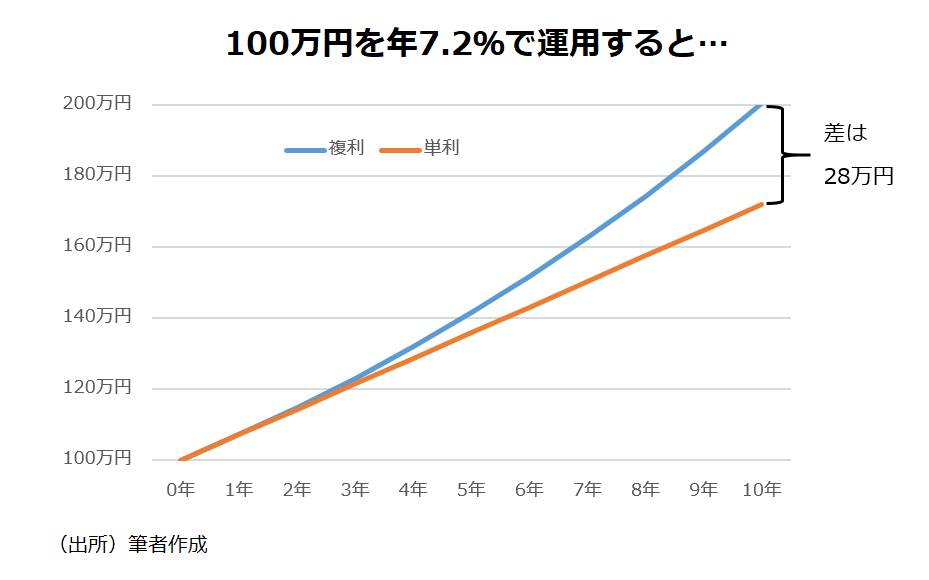
多くのケースにおいて、「複利」は「単利」との比較で語られる。前述の通り、100万円を10年で200万円にするためには年7.2%で複利運用すればよい。1年後は100万円×1.072＝107.2万円。2年後は107.2万円×1.072≒114.9万円となり、10年後に200万円に到達する。しかし「単利」だったらどうか。リターンを受け取って投資に回さない運用の結果といえるため、毎年、当初の投資額の7.2%、つまり7.2万円しか入ってこない。10年後は100万円+7.2万円×10＝172万円だ。複利と単利の差は約28万円となる。

ここまでは以前のコラムでも書いた内容だ。今回はもう少し、考え方を深めてみよう。先ほどのグラフは「年7.2%のリターンが期待できれば、10年で資産を2倍にできる」というメッセージでもある。つまりこの場合、「期待リターン=年7.2%」ということになる。先ほどのグラフのような値動きをする架空ファンドを「ファンドA」としよう。単利の累積リターンと複利の累積リターンの推移を表にすると以下のようになる。

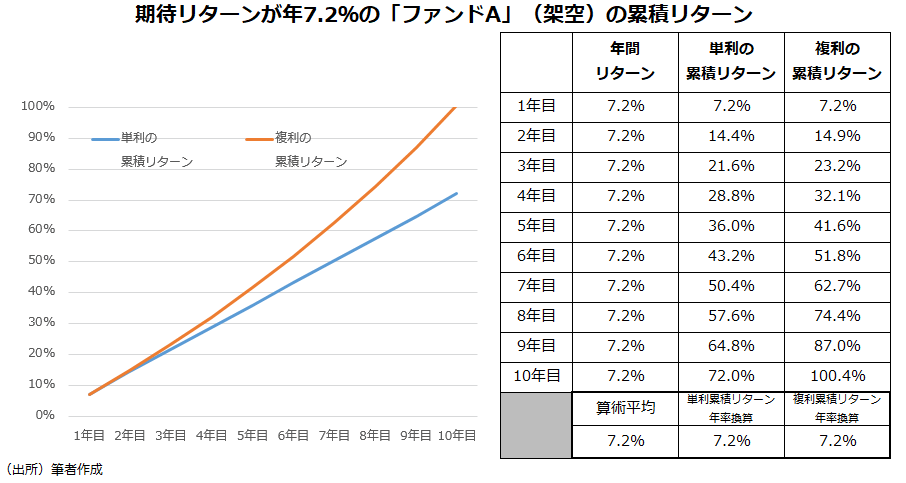
それでは、以下のような値動きをする架空の「ファンドB」については、どのように考えればよいのか。

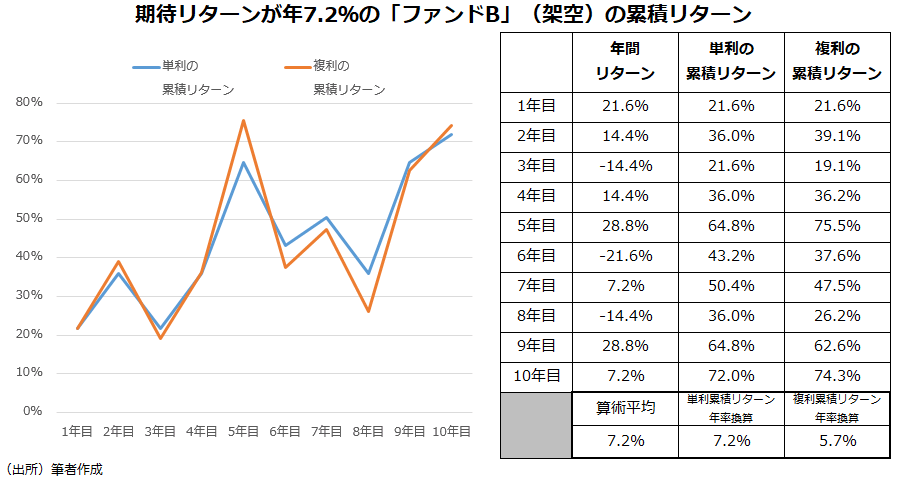
一般的な「平均」のイメージは、サンプルの数値を合計し、サンプル数で割るものだ。日常会話では「単純平均」などと言われるが、数学の世界では「算術平均」という言葉が使われる(「相加平均」とも呼ばれる)。「ファンドA」と「ファンドB」のどちらも10年間の年間リターンの算術平均が同じ「7.2%」だ。「単利」の累積リターンは算術平均の考え方なので、その年率換算値は、年間リターンの算術平均と同じ「7.2%」になる。

次に複利の累積リターンを考えてみよう。「ファンドA」は、前述の通り、10年で2倍になっている。2倍はリターンで言えば「100%」だ。一方、「ファンドB」の、複利の累積リターンは「74%」になってしまう。年間リターンの算術平均(単利の累積リターンの年率換算値)は同じなのに、なぜ、「ファンドA」と「ファンドB」にこのような差が付くのだろうか。

その謎解きに行く前に、「算術平均」とは異なる「幾何平均」という概念について説明したい。サンプルが2つの場合、算術平均はその2つを足して2で割るのに対し、幾何平均は2つを乗じて、その値の平方根(√)をとる(「幾何平均」は「相乗平均」とも呼ぶ)。

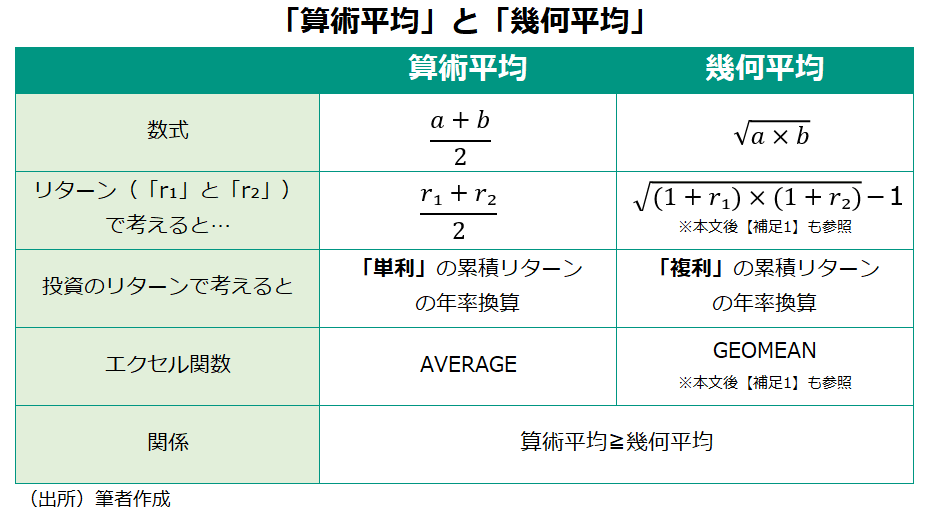
少し、頭がこんがらがってしまった人もいるかもしれないが、運用パフォーマンス評価の世界に置き換えれば、「算術平均は単利の累積リターンの年率換算値」なのに対し、「幾何平均は複利の累積リターンの年率換算値」と覚えておけば問題ないだろう。実は数学的には「算術平均≧幾何平均」という関係が成立する。それゆえ、幾何平均≒複利効果は時に棄損されてしまうことになるのだ(※補足2)。

もう一度、「ファンドA」と「ファンドB」のグラフを見比べてほしい。両者の違いは一目瞭然だ。ファンドAは毎年同じリターンでブレがない。つまり、価格変動リスクはゼロだ。一方、ファンドBは年によってリターンに大きなばらつきがあり、価格変動リスクが大きい。実は価格変動リスク(ボラティリティ)が複利効果を左右する要因になる。ファンドAのように価格変動リスク(標準偏差および分散)がゼロの場合は「幾何平均＝算術平均」となるが、価格変動リスクが大きいほど、算術平均に比べ、幾何平均が小さくなっていく。

以上を踏まえ、どんなことに注意すればよいのか。仮に、あるファンドに対する期待リターンを過去の年間リターンの算術平均から求めたとしよう。その期待リターンをもとに、将来の複利の累積リターンを推計してしまうと、将来見込まれる成果を過大評価してしまうことにもなってしまうのだ(※補足3)。

そういう意味では、過去の複利の累積リターンから、将来の期待リターンを求める方が、実態に近く適切なのかもしれない。ただ、筆者には1つ、ひっかかるところがある。多くの人が単年のリターンを考える時にイメージするのは、複利(幾何平均)ではなく、単利(算術平均)なのではないかということだ。

分かりやすさを優先して、敢えて大きな数字を使う。リターンが1年目「100%」、2年目「-50%」のファンドがあったとしよう。仮にこれだけの情報しかない場合、その後の年間リターンについて、以下のように単純に期待するだろう。

(100%+(-50%))÷2=25%

しかし、幾何平均の考え方だとどうなるか。まずは、複利の累積リターンで考えてみよう。

(1+1)×(1-0.5)-1=0%

答えは「0%」で、平方根をとって(より正確に言えば、「1」を足して平方根をとって「1」を引く)、幾何平均を求めても同じ「0%」になる。元手が2倍になって半分になる、つまり元に戻るだけなので、複利のリターンは「0%」で当たり前なのだが、「100%」と「50%」というリターンの絶対値の差を考えると、「0%」が期待リターンとして納得できる人は少ないのではないか。

【関連リンク】理解すればみんなファンドアナリスト！ 投信の「リターン」の算出・活用法 | 海老澤界の投信コラム

「現代ポートフォリオ理論」の帰結である「資本資産評価モデル(CAPM)」は銘柄のリターンを市場全体との感応度(β＝ベータ)で説明する考え方で、現代において、多くの投資戦略の理論的な支柱となっている。CAPMの理論が成立するためには、数多くの前提が必要であるが、その中の1つに「すべての投資家が同じ保有期間内で投資活動を行う」というものがある。つまりCAPMは、とある1期間だけのモデルということになる。

そのため、多くの運用戦略において、「リターンの連続」が複利の累積リターンであるという意識が希薄になっている可能性もある。要するに、ボラティリティが累積リターンにマイナスの効果をもたらすことが盲点になってしまっているのではないかと筆者は考える。長期投資のメリットばかりが喧伝される嫌いがあるが、こうした点を配慮した考え方の普及も必要だろう。

【関連リンク】大切だけど忘れがちな存在…「複利効果」| 海老澤界の投信コラム